PyTorch Fundamentals
An introduction to PyTorch tensors, operations, and GPU usage.
This class introduces you to PyTorch, a popular framework for building and training deep learning models. We’ll start from the ground up, covering what tensors are, how to create and manipulate them, how to speed things up with GPUs, how to get consistent results with random seeds, and how to switch between PyTorch and NumPy (another popular Python library for handling numerical data).
You do not need any prior experience in PyTorch or Python. We’ll treat this as if you’re completely new. Our main goal: by the end of this 50-minute session, you should be able to confidently create and work with PyTorch tensors, which are the fundamental building blocks of advanced neural networks.
What is PyTorch?
PyTorch is an open source machine learning and deep learning framework.
What can PyTorch be used for?
PyTorch allows you to manipulate and process data and write machine learning algorithms using Python code.
Who uses PyTorch?
Many of the world’s largest technology companies such as Meta (Facebook), Tesla and Microsoft as well as artificial intelligence research companies such as OpenAI use PyTorch to power research and bring machine learning to their products.
For example, Andrej Karpathy (head of AI at Tesla) has given several talks (PyTorch DevCon 2019, Tesla AI Day 2021) about how Tesla uses PyTorch to power their self-driving computer vision models.
PyTorch is also used in other industries such as agriculture to power computer vision on tractors.
Why use PyTorch?
Machine learning researchers love using PyTorch. And as of February 2022, PyTorch is the most used deep learning framework on Papers With Code, a website for tracking machine learning research papers and the code repositories attached with them.
PyTorch also helps take care of many things such as GPU acceleration (making your code run faster) behind the scenes.
So you can focus on manipulating data and writing algorithms and PyTorch will make sure it runs fast.
And if companies such as Tesla and Meta (Facebook) use it to build models they deploy to power hundreds of applications, drive thousands of cars and deliver content to billions of people, it’s clearly capable on the development front too.
What we’re going to cover in this module
This course is broken down into different sections (notebooks).
Each notebook covers important ideas and concepts within PyTorch.
Subsequent notebooks build upon knowledge from the previous one (numbering starts at 00, 01, 02 and goes to whatever it ends up going to).
This notebook deals with the basic building block of machine learning and deep learning, the tensor.
Specifically, we’re going to cover:
| Topic | Contents |
|---|---|
| Introduction to tensors | Tensors are the basic building block of all of machine learning and deep learning. |
| Creating tensors | Tensors can represent almost any kind of data (images, words, tables of numbers). |
| Getting information from tensors | If you can put information into a tensor, you'll want to get it out too. |
| Manipulating tensors | Machine learning algorithms (like neural networks) involve manipulating tensors in many different ways such as adding, multiplying, combining. |
| Dealing with tensor shapes | One of the most common issues in machine learning is dealing with shape mismatches (trying to mix wrong shaped tensors with other tensors). |
| Indexing on tensors | If you've indexed on a Python list or NumPy array, it's very similar with tensors, except they can have far more dimensions. |
| Mixing PyTorch tensors and NumPy | PyTorch plays with tensors (torch.Tensor), NumPy likes arrays (np.ndarray) sometimes you'll want to mix and match these. |
| Reproducibility | Machine learning is very experimental and since it uses a lot of randomness to work, sometimes you'll want that randomness to not be so random. |
| Running tensors on GPU | GPUs (Graphics Processing Units) make your code faster, PyTorch makes it easy to run your code on GPUs. |
Importing PyTorch
Before running any of the code in this notebook, you should have gone through the PyTorch setup steps.
If you're running on Google Colab, everything should work as is, since Google Colab comes with PyTorch and other necessary libraries pre-installed.
Let’s start by importing PyTorch and checking the version we’re using.
1
2
import torch
torch.__version__
echo '1.13.1+cu116'Wonderful, it looks like we’ve got PyTorch 1.10.0+.
This means if you’re going through these materials, you’ll see most compatability with PyTorch 1.10.0+, however if your version number is far higher than that, you might notice some inconsistencies.
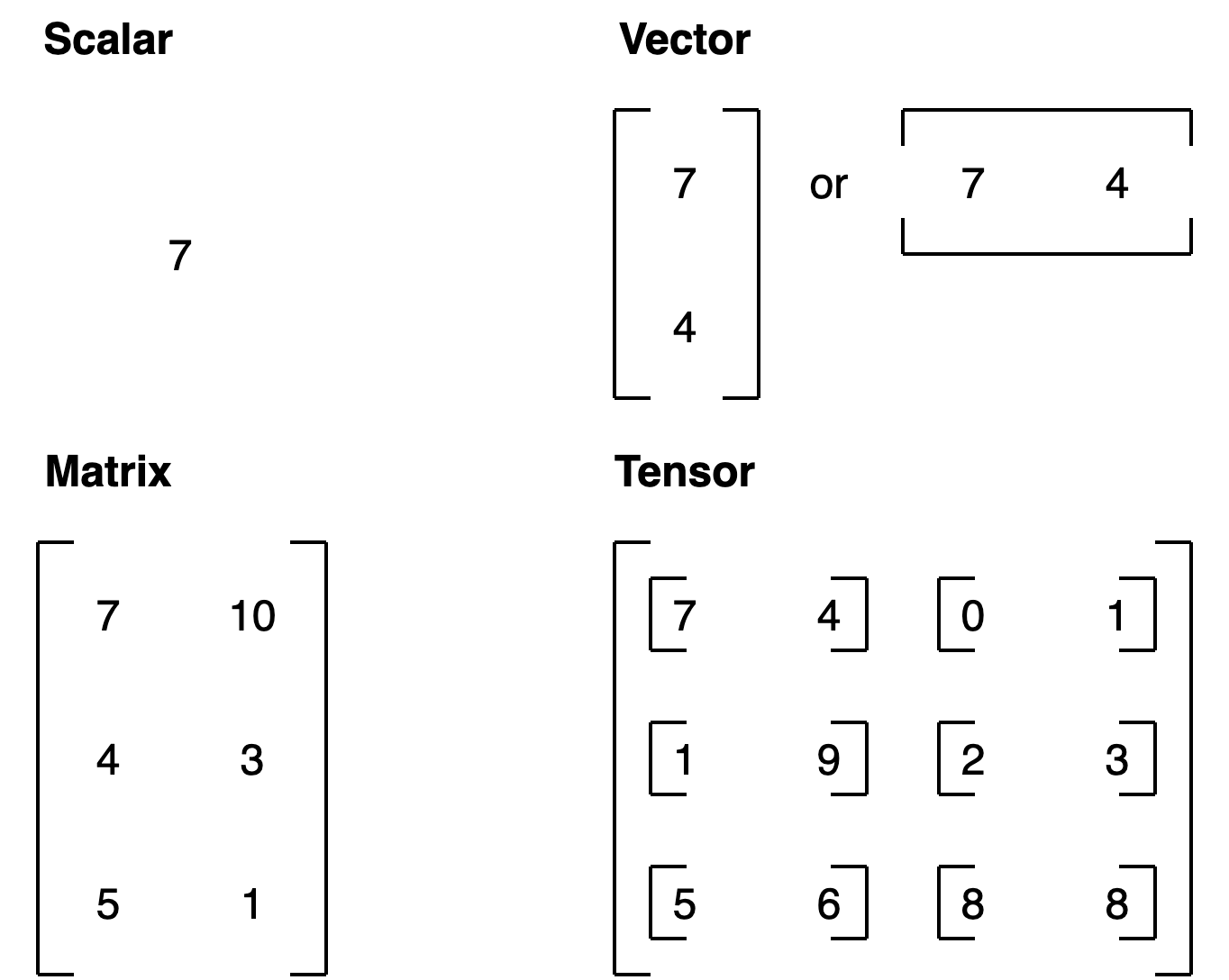
Introduction to tensors
Now we’ve got PyTorch imported, it’s time to learn about tensors.
Tensors are the fundamental building block of machine learning.
Their job is to represent data in a numerical way.
For example, you could represent an image as a tensor with shape [3, 224, 224] which would mean [colour_channels, height, width], as in the image has 3 colour channels (red, green, blue), a height of 224 pixels and a width of 224 pixels.
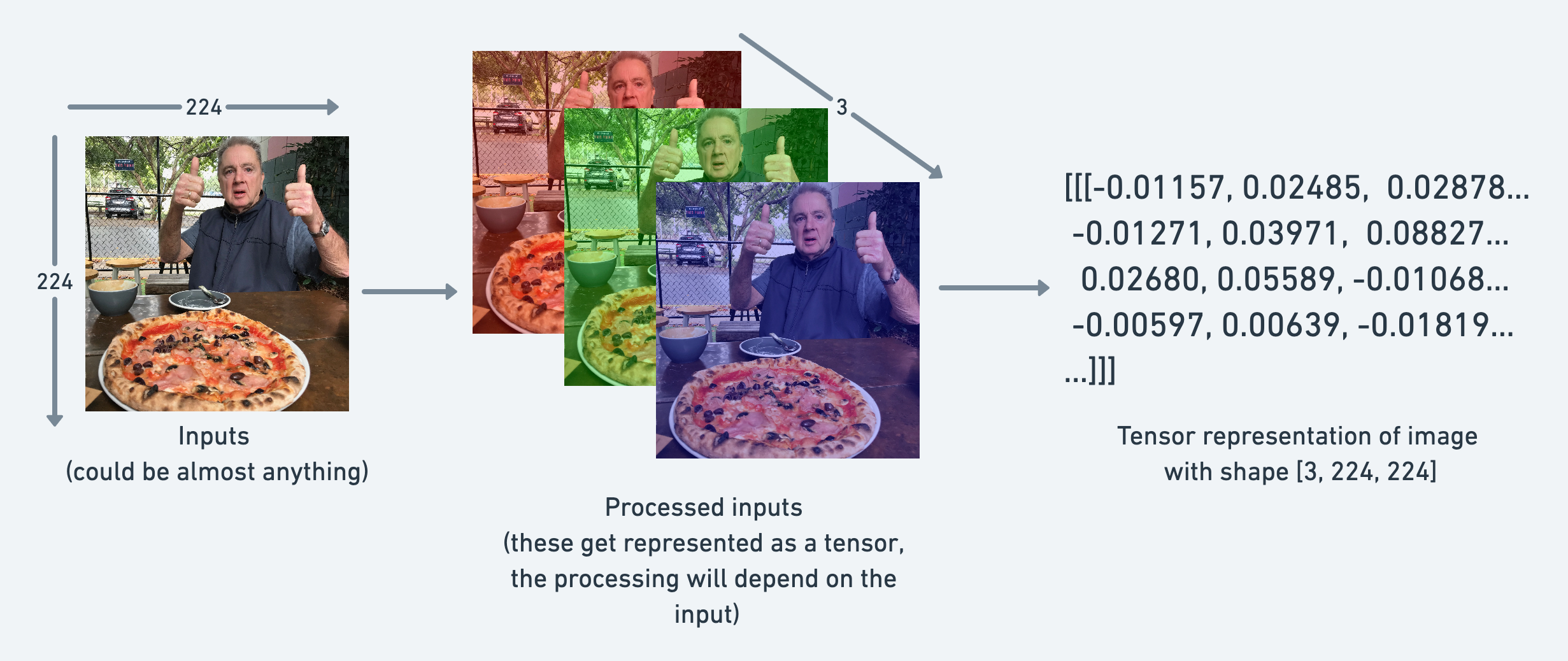
In tensor-speak (the language used to describe tensors), the tensor would have three dimensions, one for colour_channels, height and width.
But we’re getting ahead of ourselves.
Let’s learn more about tensors by coding them.
Creating tensors
PyTorch loves tensors. So much so there’s a whole documentation page dedicated to the torch.Tensor class.
Your first piece of homework is to read through the documentation on torch.Tensor for 10-minutes. But you can get to that later.
Let’s code.
The first thing we’re going to create is a scalar.
A scalar is a single number and in tensor-speak it’s a zero dimension tensor.
1
2
3
# Scalar
scalar = torch.tensor(7)
scalar
tensor(7)See how the above printed out tensor(7)?
That means although scalar is a single number, it’s of type torch.Tensor.
We can check the dimensions of a tensor using the ndim attribute.
1
scalar.ndim
0What if we wanted to retrieve the number from the tensor?
As in, turn it from torch.Tensor to a Python integer?
To do we can use the item() method.
1
2
# Get the Python number within a tensor (only works with one-element tensors)
scalar.item()
7Okay, now let’s see a vector.
A vector is a single dimension tensor but can contain many numbers.
As in, you could have a vector [3, 2] to describe [bedrooms, bathrooms] in your house. Or you could have [3, 2, 2] to describe [bedrooms, bathrooms, car_parks] in your house.
The important trend here is that a vector is flexible in what it can represent (the same with tensors).
1
2
3
# Vector
vector = torch.tensor([7, 7])
vector
tensor([7, 7])Wonderful, vector now contains two 7’s, my favourite number.
How many dimensions do you think it’ll have?
1
2
# Check the number of dimensions of vector
vector.ndim
1Hmm, that’s strange, vector contains two numbers but only has a single dimension.
I’ll let you in on a trick.
You can tell the number of dimensions a tensor in PyTorch has by the number of square brackets on the outside ([) and you only need to count one side.
How many square brackets does vector have?
Another important concept for tensors is their shape attribute. The shape tells you how the elements inside them are arranged.
Let’s check out the shape of vector.
1
2
# Check shape of vector
vector.shape
torch.Size([2])The above returns torch.Size([2]) which means our vector has a shape of [2]. This is because of the two elements we placed inside the square brackets ([7, 7]).
Let’s now see a matrix.
1
2
3
4
# Matrix
MATRIX = torch.tensor([[7, 8],
[9, 10]])
MATRIX
tensor([[ 7, 8],
[ 9, 10]])Wow! More numbers! Matrices are as flexible as vectors, except they’ve got an extra dimension.
1
2
# Check number of dimensions
MATRIX.ndim
2MATRIX has two dimensions (did you count the number of square brackets on the outside of one side?).
What shape do you think it will have?
1
MATRIX.shape
torch.Size([2, 2])We get the output torch.Size([2, 2]) because MATRIX is two elements deep and two elements wide.
How about we create a tensor?
1
2
3
4
5
# Tensor
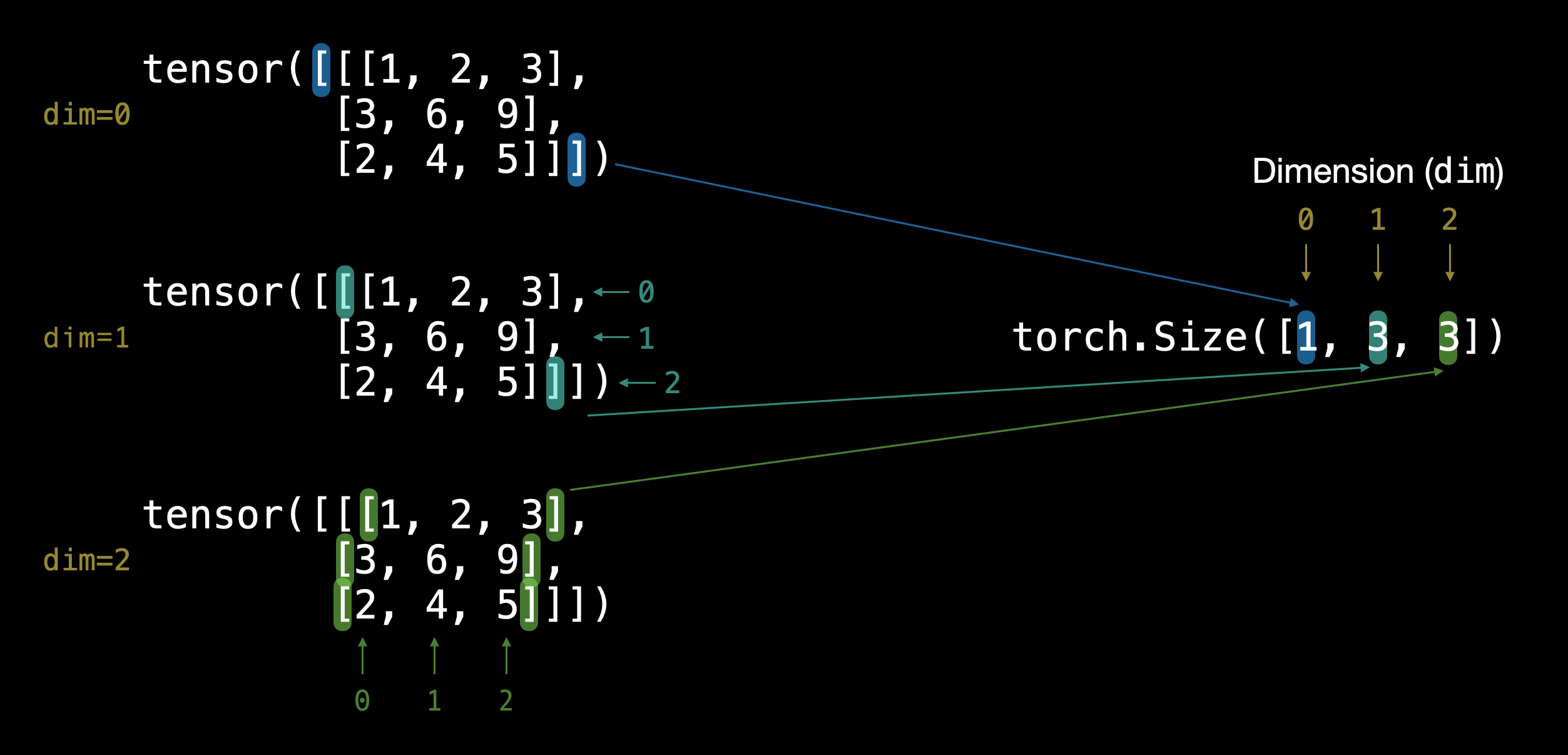
TENSOR = torch.tensor([[[1, 2, 3],
[3, 6, 9],
[2, 4, 5]]])
TENSOR
tensor([[[1, 2, 3],
[3, 6, 9],
[2, 4, 5]]])Woah! What a nice looking tensor.
I want to stress that tensors can represent almost anything.
The one we just created could be the sales numbers for a steak and almond butter store (two of my favourite foods).
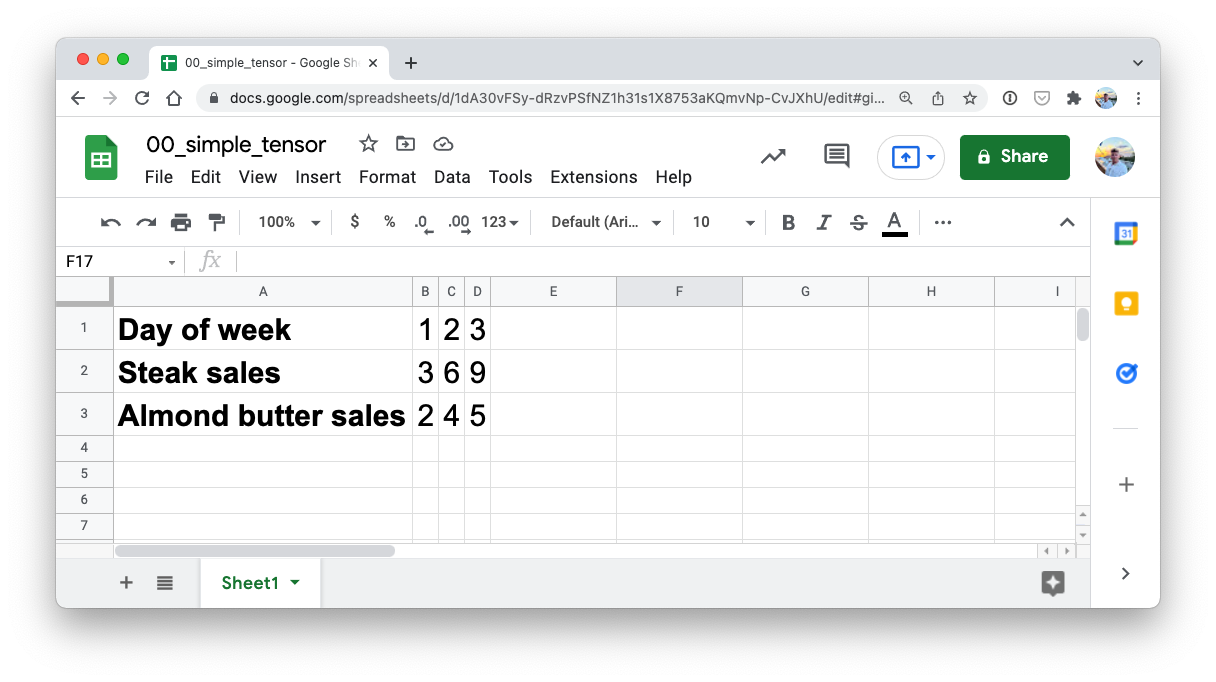
How many dimensions do you think it has? (hint: use the square bracket counting trick)
1
2
# Check number of dimensions for TENSOR
TENSOR.ndim
3And what about its shape?
1
2
# Check shape of TENSOR
TENSOR.shape
torch.Size([1, 3, 3])Alright, it outputs torch.Size([1, 3, 3]).
The dimensions go outer to inner.
That means there’s 1 dimension of 3 by 3.
Note: You might've noticed me using lowercase letters for scalar and vector and uppercase letters for MATRIX and TENSOR. This was on purpose. In practice, you'll often see scalars and vectors denoted as lowercase letters such as y or a. And matrices and tensors denoted as uppercase letters such as X or W.
You also might notice the names "matrix" and "tensor" used interchangeably. This is common. Since in PyTorch you're often dealing with torch.Tensors (hence the tensor name), the shape and dimensions of what's inside will dictate what it actually is.
Let’s summarise.
| Name | What is it? | Number of dimensions | Lower or upper (usually/example) |
|---|---|---|---|
| scalar | a single number | 0 | Lower (a) |
| vector | a number with direction (e.g. wind speed with direction) but can also have many other numbers | 1 | Lower (y) |
| matrix | a 2-dimensional array of numbers | 2 | Upper (Q) |
| tensor | an n-dimensional array of numbers | can be any number, a 0-dimension tensor is a scalar, a 1-dimension tensor is a vector | Upper (X) |
Random tensors
We’ve established tensors represent some form of data.
And machine learning models such as neural networks manipulate and seek patterns within tensors.
But when building machine learning models with PyTorch, it’s rare you’ll create tensors by hand (like what we’ve been doing).
Instead, a machine learning model often starts out with large random tensors of numbers and adjusts these random numbers as it works through data to better represent it.
In essence:
Start with random numbers -> look at data -> update random numbers -> look at data -> update random numbers...
As a data scientist, you can define how the machine learning model starts (initialization), looks at data (representation) and updates (optimization) its random numbers.
We’ll get hands on with these steps later on.
For now, let’s see how to create a tensor of random numbers.
We can do so using torch.rand() and passing in the size parameter.
1
2
3
# Create a random tensor of size (3, 4)
random_tensor = torch.rand(size=(3, 4))
random_tensor, random_tensor.dtype
(tensor([[0.6541, 0.4807, 0.2162, 0.6168],
[0.4428, 0.6608, 0.6194, 0.8620],
[0.2795, 0.6055, 0.4958, 0.5483]]),
torch.float32)The flexibility of torch.rand() is that we can adjust the size to be whatever we want.
For example, say you wanted a random tensor in the common image shape of [224, 224, 3] ([height, width, color_channels]).
1
2
3
# Create a random tensor of size (224, 224, 3)
random_image_size_tensor = torch.rand(size=(224, 224, 3))
random_image_size_tensor.shape, random_image_size_tensor.ndim
(torch.Size([224, 224, 3]), 3)Zeros and ones
Sometimes you’ll just want to fill tensors with zeros or ones.
This happens a lot with masking (like masking some of the values in one tensor with zeros to let a model know not to learn them).
Let’s create a tensor full of zeros with torch.zeros()
Again, the size parameter comes into play.
1
2
3
# Create a tensor of all zeros
zeros = torch.zeros(size=(3, 4))
zeros, zeros.dtype
(tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]),
torch.float32)We can do the same to create a tensor of all ones except using torch.ones() instead.
1
2
3
# Create a tensor of all ones
ones = torch.ones(size=(3, 4))
ones, ones.dtype
(tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]),
torch.float32)Creating a range and tensors like
Sometimes you might want a range of numbers, such as 1 to 10 or 0 to 100.
You can use torch.arange(start, end, step) to do so.
Where:
-
start= start of range (e.g. 0) -
end= end of range (e.g. 10) -
step= how many steps in between each value (e.g. 1)
range() to create a range. However, in PyTorch, torch.range() is deprecated and may show an error in the future.
1
2
3
4
5
6
# Use torch.arange(), torch.range() is deprecated
zero_to_ten_deprecated = torch.range(0, 10) # Note: this may return an error in the future
# Create a range of values 0 to 10
zero_to_ten = torch.arange(start=0, end=10, step=1)
zero_to_ten
/tmp/ipykernel_3695928/193451495.py:2: UserWarning: torch.range is deprecated and will be removed in a future release because its behavior is inconsistent with Python's range builtin. Instead, use torch.arange, which produces values in [start, end).
zero_to_ten_deprecated = torch.range(0, 10) # Note: this may return an error in the future
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])Sometimes you might want one tensor of a certain type with the same shape as another tensor.
For example, a tensor of all zeros with the same shape as a previous tensor.
To do so you can use torch.zeros_like(input) or torch.ones_like(input) which return a tensor filled with zeros or ones in the same shape as the input respectively.
1
2
3
# Can also create a tensor of zeros similar to another tensor
ten_zeros = torch.zeros_like(input=zero_to_ten) # will have same shape
ten_zeros
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])Tensor datatypes
There are many different tensor datatypes available in PyTorch.
Some are specific for CPU and some are better for GPU.
Getting to know which one can take some time.
Generally if you see torch.cuda anywhere, the tensor is being used for GPU (since Nvidia GPUs use a computing toolkit called CUDA).
The most common type (and generally the default) is torch.float32 or torch.float.
This is referred to as “32-bit floating point”.
But there’s also 16-bit floating point (torch.float16 or torch.half) and 64-bit floating point (torch.float64 or torch.double).
And to confuse things even more there’s also 8-bit, 16-bit, 32-bit and 64-bit integers.
Plus more!
7 whereas a float has a decimal 7.0. The reason for all of these is to do with precision in computing.
Precision is the amount of detail used to describe a number.
The higher the precision value (8, 16, 32), the more detail and hence data used to express a number.
This matters in deep learning and numerical computing because you’re making so many operations, the more detail you have to calculate on, the more compute you have to use.
So lower precision datatypes are generally faster to compute on but sacrifice some performance on evaluation metrics like accuracy (faster to compute but less accurate).
Let’s see how to create some tensors with specific datatypes. We can do so using the dtype parameter.
1
2
3
4
5
6
7
# Default datatype for tensors is float32
float_32_tensor = torch.tensor([3.0, 6.0, 9.0],
dtype=None, # defaults to None, which is torch.float32 or whatever datatype is passed
device=None, # defaults to None, which uses the default tensor type
requires_grad=False) # if True, operations performed on the tensor are recorded
float_32_tensor.shape, float_32_tensor.dtype, float_32_tensor.device
(torch.Size([3]), torch.float32, device(type='cpu'))Aside from shape issues (tensor shapes don’t match up), two of the other most common issues you’ll come across in PyTorch are datatype and device issues.
For example, one of tensors is torch.float32 and the other is torch.float16 (PyTorch often likes tensors to be the same format).
Or one of your tensors is on the CPU and the other is on the GPU (PyTorch likes calculations between tensors to be on the same device).
We’ll see more of this device talk later on.
For now let’s create a tensor with dtype=torch.float16.
1
2
3
4
float_16_tensor = torch.tensor([3.0, 6.0, 9.0],
dtype=torch.float16) # torch.half would also work
float_16_tensor.dtype
torch.float16Getting information from tensors
Once you’ve created tensors (or someone else or a PyTorch module has created them for you), you might want to get some information from them.
We’ve seen these before but three of the most common attributes you’ll want to find out about tensors are:
-
shape- what shape is the tensor? (some operations require specific shape rules) -
dtype- what datatype are the elements within the tensor stored in? -
device- what device is the tensor stored on? (usually GPU or CPU)
Let’s create a random tensor and find out details about it.
1
2
3
4
5
6
7
8
# Create a tensor
some_tensor = torch.rand(3, 4)
# Find out details about it
print(some_tensor)
print(f"Shape of tensor: {some_tensor.shape}")
print(f"Datatype of tensor: {some_tensor.dtype}")
print(f"Device tensor is stored on: {some_tensor.device}") # will default to CPU
tensor([[0.4688, 0.0055, 0.8551, 0.0646],
[0.6538, 0.5157, 0.4071, 0.2109],
[0.9960, 0.3061, 0.9369, 0.7008]])
Shape of tensor: torch.Size([3, 4])
Datatype of tensor: torch.float32
Device tensor is stored on: cpu- what shape are my tensors? what datatype are they and where are they stored? what shape, what datatype, where where where
Manipulating tensors (tensor operations)
In deep learning, data (images, text, video, audio, protein structures, etc) gets represented as tensors.
A model learns by investigating those tensors and performing a series of operations (could be 1,000,000s+) on tensors to create a representation of the patterns in the input data.
These operations are often a wonderful dance between:
- Addition
- Substraction
- Multiplication (element-wise)
- Division
- Matrix multiplication
And that’s it. Sure there are a few more here and there but these are the basic building blocks of neural networks.
Stacking these building blocks in the right way, you can create the most sophisticated of neural networks (just like lego!).
Basic operations
Let’s start with a few of the fundamental operations, addition (+), subtraction (-), mutliplication (*).
They work just as you think they would.
1
2
3
# Create a tensor of values and add a number to it
tensor = torch.tensor([1, 2, 3])
tensor + 10
tensor([11, 12, 13])
1
2
# Multiply it by 10
tensor * 10
tensor([10, 20, 30])Notice how the tensor values above didn’t end up being tensor([110, 120, 130]), this is because the values inside the tensor don’t change unless they’re reassigned.
1
2
# Tensors don't change unless reassigned
tensor
tensor([1, 2, 3])Let’s subtract a number and this time we’ll reassign the tensor variable.
1
2
3
# Subtract and reassign
tensor = tensor - 10
tensor
tensor([-9, -8, -7])
1
2
3
# Add and reassign
tensor = tensor + 10
tensor
tensor([1, 2, 3])PyTorch also has a bunch of built-in functions like torch.mul() (short for multiplication) and torch.add() to perform basic operations.
1
2
# Can also use torch functions
torch.multiply(tensor, 10)
tensor([10, 20, 30])
1
2
# Original tensor is still unchanged
tensor
tensor([1, 2, 3])However, it’s more common to use the operator symbols like * instead of torch.mul()
1
2
3
# Element-wise multiplication (each element multiplies its equivalent, index 0->0, 1->1, 2->2)
print(tensor, "*", tensor)
print("Equals:", tensor * tensor)
tensor([1, 2, 3]) * tensor([1, 2, 3])
Equals: tensor([1, 4, 9])Matrix multiplication (is all you need)
One of the most common operations in machine learning and deep learning algorithms (like neural networks) is matrix multiplication.
PyTorch implements matrix multiplication functionality in the torch.matmul() method.
The main two rules for matrix multiplication to remember are:
- The inner dimensions must match:
-
(3, 2) @ (3, 2)won’t work -
(2, 3) @ (3, 2)will work -
(3, 2) @ (2, 3)will work
-
- The resulting matrix has the shape of the outer dimensions:
-
(2, 3) @ (3, 2)->(2, 2) -
(3, 2) @ (2, 3)->(3, 3)
-
- Note: "
@" in Python is the symbol for matrix multiplication. - Resource: See the rules for matrix multiplication using
torch.matmul()in the PyTorch documentation.
Let’s create a tensor and perform element-wise multiplication and matrix multiplication on it.
1
2
3
import torch
tensor = torch.tensor([1, 2, 3])
tensor.shape
torch.Size([3])The difference between element-wise multiplication and matrix multiplication is the addition of values.
For our tensor variable with values [1, 2, 3]:
| Operation | Calculation | Code |
|---|---|---|
| Element-wise multiplication | [1*1, 2*2, 3*3] = [1, 4, 9] | tensor * tensor |
| Matrix multiplication | [1*1 + 2*2 + 3*3] = [14] | tensor.matmul(tensor) |
1
2
# Element-wise matrix multiplication
tensor * tensor
tensor([1, 4, 9])
1
2
# Matrix multiplication
torch.matmul(tensor, tensor)
tensor(14)
1
2
# Can also use the "@" symbol for matrix multiplication, though not recommended
tensor @ tensor
tensor(14)You can do matrix multiplication by hand but it’s not recommended.
The in-built torch.matmul() method is faster.
1
2
3
4
5
6
7
%%time
# Matrix multiplication by hand
# (avoid doing operations with for loops at all cost, they are computationally expensive)
value = 0
for i in range(len(tensor)):
value += tensor[i] * tensor[i]
value
CPU times: user 773 µs, sys: 0 ns, total: 773 µs
Wall time: 499 µs
tensor(14)
1
2
%%time
torch.matmul(tensor, tensor)
CPU times: user 146 µs, sys: 83 µs, total: 229 µs
Wall time: 171 µs
tensor(14)One of the most common errors in deep learning (shape errors)
Because much of deep learning is multiplying and performing operations on matrices and matrices have a strict rule about what shapes and sizes can be combined, one of the most common errors you’ll run into in deep learning is shape mismatches.
1
2
3
4
5
6
7
8
9
10
# Shapes need to be in the right way
tensor_A = torch.tensor([[1, 2],
[3, 4],
[5, 6]], dtype=torch.float32)
tensor_B = torch.tensor([[7, 10],
[8, 11],
[9, 12]], dtype=torch.float32)
torch.matmul(tensor_A, tensor_B) # (this will error)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
tensor_A = torch.tensor([[1, 2],
[3, 4],
[5, 6]], dtype=torch.float32)
tensor_B = torch.tensor([[7, 10],
[8, 11],
[9, 12]], dtype=torch.float32)
torch.matmul(tensor_A, tensor_B)
RuntimeError: mat1 and mat2 shapes cannot be multiplied (3x2 and 3x2)We can make matrix multiplication work between tensor_A and tensor_B by making their inner dimensions match.
One of the ways to do this is with a transpose (switch the dimensions of a given tensor).
You can perform transposes in PyTorch using either:
-
torch.transpose(input, dim0, dim1)- whereinputis the desired tensor to transpose anddim0anddim1are the dimensions to be swapped. -
tensor.T- wheretensoris the desired tensor to transpose.
Let’s try the latter.
1
2
3
# View tensor_A and tensor_B
print(tensor_A)
print(tensor_B)
tensor([[1., 2.],
[3., 4.],
[5., 6.]])
tensor([[ 7., 10.],
[ 8., 11.],
[ 9., 12.]])
1
2
3
# View tensor_A and tensor_B.T
print(tensor_A)
print(tensor_B.T)
tensor([[1., 2.],
[3., 4.],
[5., 6.]])
tensor([[ 7., 8., 9.],
[10., 11., 12.]])
1
2
3
4
5
6
7
8
# The operation works when tensor_B is transposed
print(f"Original shapes: tensor_A = {tensor_A.shape}, tensor_B = {tensor_B.shape}\n")
print(f"New shapes: tensor_A = {tensor_A.shape} (same as above), tensor_B.T = {tensor_B.T.shape}\n")
print(f"Multiplying: {tensor_A.shape} * {tensor_B.T.shape} <- inner dimensions match\n")
print("Output:\n")
output = torch.matmul(tensor_A, tensor_B.T)
print(output)
print(f"\nOutput shape: {output.shape}")
Original shapes: tensor_A = torch.Size([3, 2]), tensor_B = torch.Size([3, 2])
New shapes: tensor_A = torch.Size([3, 2]) (same as above), tensor_B.T = torch.Size([2, 3])
Multiplying: torch.Size([3, 2]) * torch.Size([2, 3]) <- inner dimensions match
Output:
tensor([[ 27., 30., 33.],
[ 61., 68., 75.],
[ 95., 106., 117.]])
Output shape: torch.Size([3, 3])You can also use torch.mm() which is a short for torch.matmul().
1
2
# torch.mm is a shortcut for matmul
torch.mm(tensor_A, tensor_B.T)
tensor([[ 27., 30., 33.],
[ 61., 68., 75.],
[ 95., 106., 117.]])Without the transpose, the rules of matrix multiplication aren’t fulfilled and we get an error like above.
How about a visual?

You can create your own matrix multiplication visuals like this at http://matrixmultiplication.xyz/.
Neural networks are full of matrix multiplications and dot products.
The torch.nn.Linear() module (we’ll see this in action later on), also known as a feed-forward layer or fully connected layer, implements a matrix multiplication between an input x and a weights matrix A.
Where:
-
xis the input to the layer (deep learning is a stack of layers liketorch.nn.Linear()and others on top of each other). -
Ais the weights matrix created by the layer, this starts out as random numbers that get adjusted as a neural network learns to better represent patterns in the data (notice the “T”, that’s because the weights matrix gets transposed).- Note: You might also often see
Wor another letter likeXused to showcase the weights matrix.
- Note: You might also often see
-
bis the bias term used to slightly offset the weights and inputs. -
yis the output (a manipulation of the input in the hopes to discover patterns in it).
This is a linear function (you may have seen something like $y = mx+b$ in high school or elsewhere), and can be used to draw a straight line!
Let’s play around with a linear layer.
Try changing the values of in_features and out_features below and see what happens.
Do you notice anything to do with the shapes?
1
2
3
4
5
6
7
8
9
# Since the linear layer starts with a random weights matrix, let's make it reproducible (more on this later)
torch.manual_seed(42)
# This uses matrix multiplication
linear = torch.nn.Linear(in_features=2, # in_features = matches inner dimension of input
out_features=6) # out_features = describes outer value
x = tensor_A
output = linear(x)
print(f"Input shape: {x.shape}\n")
print(f"Output:\n{output}\n\nOutput shape: {output.shape}")
Input shape: torch.Size([3, 2])
Output:
tensor([[2.2368, 1.2292, 0.4714, 0.3864, 0.1309, 0.9838],
[4.4919, 2.1970, 0.4469, 0.5285, 0.3401, 2.4777],
[6.7469, 3.1648, 0.4224, 0.6705, 0.5493, 3.9716]],
grad_fn=<AddmmBackward0>)
Output shape: torch.Size([3, 6])in_features from 2 to 3 above? Does it error? How could you change the shape of the input (x) to accommodate the error? Hint: What did we have to do to tensor_B above? If you’ve never done it before, matrix multiplication can be a confusing topic at first.
But after you’ve played around with it a few times and even cracked open a few neural networks, you’ll notice it’s everywhere.
Remember, matrix multiplication is all you need.
When you start digging into neural network layers and building your own, you’ll find matrix multiplications everywhere. Source: Working Calss Deep Learner
Finding the min, max, mean, sum, etc (aggregation)
Now we’ve seen a few ways to manipulate tensors, let’s run through a few ways to aggregate them (go from more values to less values).
First we’ll create a tensor and then find the max, min, mean and sum of it.
1
2
3
# Create a tensor
x = torch.arange(0, 100, 10)
x
tensor([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])Now let’s perform some aggregation.
1
2
3
4
5
print(f"Minimum: {x.min()}")
print(f"Maximum: {x.max()}")
# print(f"Mean: {x.mean()}") # this will error
print(f"Mean: {x.type(torch.float32).mean()}") # won't work without float datatype
print(f"Sum: {x.sum()}")
Minimum: 0
Maximum: 90
Mean: 45.0
Sum: 450torch.mean() require tensors to be in torch.float32 (the most common) or another specific datatype, otherwise the operation will fail. You can also do the same as above with torch methods.
1
torch.max(x), torch.min(x), torch.mean(x.type(torch.float32)), torch.sum(x)
(tensor(90), tensor(0), tensor(45.), tensor(450))Positional min/max
You can also find the index of a tensor where the max or minimum occurs with torch.argmax() and torch.argmin() respectively.
This is helpful incase you just want the position where the highest (or lowest) value is and not the actual value itself (we’ll see this in a later section when using the softmax activation function).
1
2
3
4
5
6
7
# Create a tensor
tensor = torch.arange(10, 100, 10)
print(f"Tensor: {tensor}")
# Returns index of max and min values
print(f"Index where max value occurs: {tensor.argmax()}")
print(f"Index where min value occurs: {tensor.argmin()}")
Tensor: tensor([10, 20, 30, 40, 50, 60, 70, 80, 90])
Index where max value occurs: 8
Index where min value occurs: 0Change tensor datatype
As mentioned, a common issue with deep learning operations is having your tensors in different datatypes.
If one tensor is in torch.float64 and another is in torch.float32, you might run into some errors.
But there’s a fix.
You can change the datatypes of tensors using torch.Tensor.type(dtype=None) where the dtype parameter is the datatype you’d like to use.
First we’ll create a tensor and check its datatype (the default is torch.float32).
1
2
3
# Create a tensor and check its datatype
tensor = torch.arange(10., 100., 10.)
tensor.dtype
torch.float32Now we’ll create another tensor the same as before but change its datatype to torch.float16.
1
2
3
# Create a float16 tensor
tensor_float16 = tensor.type(torch.float16)
tensor_float16
tensor([10., 20., 30., 40., 50., 60., 70., 80., 90.], dtype=torch.float16)And we can do something similar to make a torch.int8 tensor.
1
2
3
# Create an int8 tensor
tensor_int8 = tensor.type(torch.int8)
tensor_int8
tensor([10, 20, 30, 40, 50, 60, 70, 80, 90], dtype=torch.int8)torch.Tensor documentation. Spend about 10 minutes scrolling through and looking into any that catch your eye. Then click on them and write them out in code yourself to see what happens. Reshaping, stacking, squeezing and unsqueezing
Often times you’ll want to reshape or change the dimensions of your tensors without actually changing the values inside them.
To do so, some popular methods are:
| Method | One-line description |
|---|---|
torch.reshape(input, shape) | Reshapes input to shape (if compatible), can also use torch.Tensor.reshape(). |
Tensor.view(shape) | Returns a view of the original tensor in a different shape but shares the same data as the original tensor. |
torch.stack(tensors, dim=0) | Concatenates a sequence of tensors along a new dimension (dim), all tensors must be the same size. |
torch.squeeze(input) | Squeezes input to remove all the dimensions with value 1. |
torch.unsqueeze(input, dim) | Returns input with a dimension value of 1 added at dim. |
torch.permute(input, dims) | Returns a view of the original input with its dimensions permuted (rearranged) to dims. |
Why do any of these?
Because deep learning models (neural networks) are all about manipulating tensors in some way. And because of the rules of matrix multiplication, if you’ve got shape mismatches, you’ll run into errors. These methods help you make sure the right elements of your tensors are mixing with the right elements of other tensors.
Let’s try them out.
First, we’ll create a tensor.
1
2
3
4
# Create a tensor
import torch
x = torch.arange(1., 8.)
x, x.shape
(tensor([1., 2., 3., 4., 5., 6., 7.]), torch.Size([7]))Now let’s add an extra dimension with torch.reshape().
1
2
3
# Add an extra dimension
x_reshaped = x.reshape(1, 7)
x_reshaped, x_reshaped.shape
(tensor([[1., 2., 3., 4., 5., 6., 7.]]), torch.Size([1, 7]))We can also change the view with torch.view().
1
2
3
4
# Change view (keeps same data as original but changes view)
# See more: https://stackoverflow.com/a/54507446/7900723
z = x.view(1, 7)
z, z.shape
(tensor([[1., 2., 3., 4., 5., 6., 7.]]), torch.Size([1, 7]))Remember though, changing the view of a tensor with torch.view() really only creates a new view of the same tensor.
So changing the view changes the original tensor too.
1
2
3
# Changing z changes x
z[:, 0] = 5
z, x
(tensor([[5., 2., 3., 4., 5., 6., 7.]]), tensor([5., 2., 3., 4., 5., 6., 7.]))If we wanted to stack our new tensor on top of itself five times, we could do so with torch.stack().
1
2
3
# Stack tensors on top of each other
x_stacked = torch.stack([x, x, x, x], dim=0) # try changing dim to dim=1 and see what happens
x_stacked
tensor([[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.]])How about removing all single dimensions from a tensor?
To do so you can use torch.squeeze() (I remember this as squeezing the tensor to only have dimensions over 1).
1
2
3
4
5
6
7
print(f"Previous tensor: {x_reshaped}")
print(f"Previous shape: {x_reshaped.shape}")
# Remove extra dimension from x_reshaped
x_squeezed = x_reshaped.squeeze()
print(f"\nNew tensor: {x_squeezed}")
print(f"New shape: {x_squeezed.shape}")
Previous tensor: tensor([[5., 2., 3., 4., 5., 6., 7.]])
Previous shape: torch.Size([1, 7])
New tensor: tensor([5., 2., 3., 4., 5., 6., 7.])
New shape: torch.Size([7])And to do the reverse of torch.squeeze() you can use torch.unsqueeze() to add a dimension value of 1 at a specific index.
1
2
3
4
5
6
7
print(f"Previous tensor: {x_squeezed}")
print(f"Previous shape: {x_squeezed.shape}")
## Add an extra dimension with unsqueeze
x_unsqueezed = x_squeezed.unsqueeze(dim=0)
print(f"\nNew tensor: {x_unsqueezed}")
print(f"New shape: {x_unsqueezed.shape}")
Previous tensor: tensor([[5., 2., 3., 4., 5., 6., 7.]])
Previous shape: torch.Size([1, 7])
New tensor: tensor([5., 2., 3., 4., 5., 6., 7.])
New shape: torch.Size([7])You can also rearrange the order of axes values with torch.permute(input, dims), where the input gets turned into a view with new dims.
1
2
3
4
5
6
7
8
# Create tensor with specific shape
x_original = torch.rand(size=(224, 224, 3))
# Permute the original tensor to rearrange the axis order
x_permuted = x_original.permute(2, 0, 1) # shifts axis 0->1, 1->2, 2->0
print(f"Previous shape: {x_original.shape}")
print(f"New shape: {x_permuted.shape}")
Previous shape: torch.Size([224, 224, 3])
New shape: torch.Size([3, 224, 224])Indexing (selecting data from tensors)
Sometimes you’ll want to select specific data from tensors (for example, only the first column or second row).
To do so, you can use indexing.
If you’ve ever done indexing on Python lists or NumPy arrays, indexing in PyTorch with tensors is very similar.
1
2
3
4
# Create a tensor
import torch
x = torch.arange(1, 10).reshape(1, 3, 3)
x, x.shape
(tensor([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]]),
torch.Size([1, 3, 3]))Indexing values goes outer dimension -> inner dimension (check out the square brackets).
1
2
3
4
# Let's index bracket by bracket
print(f"First square bracket:\n{x[0]}")
print(f"Second square bracket: {x[0][0]}")
print(f"Third square bracket: {x[0][0][0]}")
First square bracket:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
Second square bracket: tensor([1, 2, 3])
Third square bracket: 1You can also use : to specify “all values in this dimension” and then use a comma (,) to add another dimension.
1
2
# Get all values of 0th dimension and the 0 index of 1st dimension
x[:, 0]
tensor([[1, 2, 3]])
1
2
# Get all values of 0th & 1st dimensions but only index 1 of 2nd dimension
x[:, :, 1]
tensor([[2, 5, 8]])
1
2
# Get all values of the 0 dimension but only the 1 index value of the 1st and 2nd dimension
x[:, 1, 1]
tensor([5])
1
2
# Get index 0 of 0th and 1st dimension and all values of 2nd dimension
x[0, 0, :] # same as x[0][0]
tensor([1, 2, 3])Indexing can be quite confusing to begin with, especially with larger tensors (I still have to try indexing multiple times to get it right). But with a bit of practice and following the data explorer’s motto (visualize, visualize, visualize), you’ll start to get the hang of it.
PyTorch tensors & NumPy
Since NumPy is a popular Python numerical computing library, PyTorch has functionality to interact with it nicely.
The two main methods you’ll want to use for NumPy to PyTorch (and back again) are:
-
torch.from_numpy(ndarray)- NumPy array -> PyTorch tensor. -
torch.Tensor.numpy()- PyTorch tensor -> NumPy array.
Let’s try them out.
1
2
3
4
5
6
# NumPy array to tensor
import torch
import numpy as np
array = np.arange(1.0, 8.0)
tensor = torch.from_numpy(array)
array, tensor
(array([1., 2., 3., 4., 5., 6., 7.]),
tensor([1., 2., 3., 4., 5., 6., 7.], dtype=torch.float64))float64 and if you convert it to a PyTorch tensor, it'll keep the same datatype (as above). However, many PyTorch calculations default to using float32. So if you want to convert your NumPy array (float64) → PyTorch tensor (float64) → PyTorch tensor (float32), you can use: tensor = torch.from_numpy(array).type(torch.float32)Because we reassigned tensor above, if you change the tensor, the array stays the same.
1
2
3
# Change the array, keep the tensor
array = array + 1
array, tensor
(array([2., 3., 4., 5., 6., 7., 8.]),
tensor([1., 2., 3., 4., 5., 6., 7.], dtype=torch.float64))And if you want to go from PyTorch tensor to NumPy array, you can call tensor.numpy().
1
2
3
4
# Tensor to NumPy array
tensor = torch.ones(7) # create a tensor of ones with dtype=float32
numpy_tensor = tensor.numpy() # will be dtype=float32 unless changed
tensor, numpy_tensor
(tensor([1., 1., 1., 1., 1., 1., 1.]),
array([1., 1., 1., 1., 1., 1., 1.], dtype=float32))And the same rule applies as above, if you change the original tensor, the new numpy_tensor stays the same.
1
2
3
# Change the tensor, keep the array the same
tensor = tensor + 1
tensor, numpy_tensor
(tensor([2., 2., 2., 2., 2., 2., 2.]),
array([1., 1., 1., 1., 1., 1., 1.], dtype=float32))Reproducibility (trying to take the random out of random)
As you learn more about neural networks and machine learning, you’ll start to discover how much randomness plays a part.
Well, pseudorandomness that is. Because after all, as they’re designed, a computer is fundamentally deterministic (each step is predictable) so the randomness they create are simulated randomness (though there is debate on this too, but since I’m not a computer scientist, I’ll let you find out more yourself).
How does this relate to neural networks and deep learning then?
We’ve discussed neural networks start with random numbers to describe patterns in data (these numbers are poor descriptions) and try to improve those random numbers using tensor operations (and a few other things we haven’t discussed yet) to better describe patterns in data.
In short:
start with random numbers -> tensor operations -> try to make better (again and again and again)
Although randomness is nice and powerful, sometimes you’d like there to be a little less randomness.
Why?
So you can perform repeatable experiments.
For example, you create an algorithm capable of achieving X performance.
And then your friend tries it out to verify you’re not crazy.
How could they do such a thing?
That’s where reproducibility comes in.
In other words, can you get the same (or very similar) results on your computer running the same code as I get on mine?
Let’s see a brief example of reproducibility in PyTorch.
We’ll start by creating two random tensors, since they’re random, you’d expect them to be different right?
1
2
3
4
5
6
7
8
9
10
import torch
# Create two random tensors
random_tensor_A = torch.rand(3, 4)
random_tensor_B = torch.rand(3, 4)
print(f"Tensor A:\n{random_tensor_A}\n")
print(f"Tensor B:\n{random_tensor_B}\n")
print(f"Does Tensor A equal Tensor B? (anywhere)")
random_tensor_A == random_tensor_B
Tensor A:
tensor([[0.8016, 0.3649, 0.6286, 0.9663],
[0.7687, 0.4566, 0.5745, 0.9200],
[0.3230, 0.8613, 0.0919, 0.3102]])
Tensor B:
tensor([[0.9536, 0.6002, 0.0351, 0.6826],
[0.3743, 0.5220, 0.1336, 0.9666],
[0.9754, 0.8474, 0.8988, 0.1105]])
Does Tensor A equal Tensor B? (anywhere)
tensor([[False, False, False, False],
[False, False, False, False],
[False, False, False, False]])Just as you might’ve expected, the tensors come out with different values.
But what if you wanted to create two random tensors with the same values.
As in, the tensors would still contain random values but they would be of the same flavour.
That’s where torch.manual_seed(seed) comes in, where seed is an integer (like 42 but it could be anything) that flavours the randomness.
Let’s try it out by creating some more flavoured random tensors.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
import random
# # Set the random seed
RANDOM_SEED=42 # try changing this to different values and see what happens to the numbers below
torch.manual_seed(seed=RANDOM_SEED)
random_tensor_C = torch.rand(3, 4)
# Have to reset the seed every time a new rand() is called
# Without this, tensor_D would be different to tensor_C
torch.random.manual_seed(seed=RANDOM_SEED) # try commenting this line out and seeing what happens
random_tensor_D = torch.rand(3, 4)
print(f"Tensor C:\n{random_tensor_C}\n")
print(f"Tensor D:\n{random_tensor_D}\n")
print(f"Does Tensor C equal Tensor D? (anywhere)")
random_tensor_C == random_tensor_D
Tensor C:
tensor([[0.8823, 0.9150, 0.3829, 0.9593],
[0.3904, 0.6009, 0.2566, 0.7936],
[0.9408, 0.1332, 0.9346, 0.5936]])
Tensor D:
tensor([[0.8823, 0.9150, 0.3829, 0.9593],
[0.3904, 0.6009, 0.2566, 0.7936],
[0.9408, 0.1332, 0.9346, 0.5936]])
Does Tensor C equal Tensor D? (anywhere)
tensor([[True, True, True, True],
[True, True, True, True],
[True, True, True, True]])Nice!
It looks like setting the seed worked.
- The PyTorch reproducibility documentation (a good exercise would be to read through this for 10-minutes and even if you don't understand it now, being aware of it is important).
- The Wikipedia random seed page (this'll give a good overview of random seeds and pseudorandomness in general).
Running tensors on GPUs (and making faster computations)
Deep learning algorithms require a lot of numerical operations.
And by default these operations are often done on a CPU (computer processing unit).
However, there’s another common piece of hardware called a GPU (graphics processing unit), which is often much faster at performing the specific types of operations neural networks need (matrix multiplications) than CPUs.
Your computer might have one.
If so, you should look to use it whenever you can to train neural networks because chances are it’ll speed up the training time dramatically.
There are a few ways to first get access to a GPU and secondly get PyTorch to use the GPU.
Getting a GPU
You may already know what’s going on when I say GPU. But if not, there are a few ways to get access to one.
| Method | Difficulty to setup | Pros | Cons | How to setup |
|---|---|---|---|---|
| Google Colab | Easy | Free to use, almost zero setup required, can share work with others as easy as a link | Doesn't save your data outputs, limited compute, subject to timeouts | Follow the Google Colab Guide |
| Use your own | Medium | Run everything locally on your own machine | GPUs aren't free, require upfront cost | Follow the PyTorch installation guidelines |
| Cloud computing (AWS, GCP, Azure) | Medium-Hard | Small upfront cost, access to almost infinite compute | Can get expensive if running continually, takes some time to setup right | Follow the PyTorch installation guidelines |
There are more options for using GPUs but the above three will suffice for now.
Personally, I use a combination of Google Colab and my own personal computer for small scale experiments (and creating this course) and go to cloud resources when I need more compute power.
To check if you’ve got access to a Nvidia GPU, you can run !nvidia-smi where the ! (also called bang) means “run this on the command line”.
1
!nvidia-smi
Sat Jan 21 08:34:23 2023
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 515.48.07 Driver Version: 515.48.07 CUDA Version: 11.7 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 NVIDIA TITAN RTX On | 00000000:01:00.0 Off | N/A |
| 40% 30C P8 7W / 280W | 177MiB / 24576MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| 0 N/A N/A 1061 G /usr/lib/xorg/Xorg 53MiB |
| 0 N/A N/A 2671131 G /usr/lib/xorg/Xorg 97MiB |
| 0 N/A N/A 2671256 G /usr/bin/gnome-shell 9MiB |
+-----------------------------------------------------------------------------+
If you don’t have a Nvidia GPU accessible, the above will output something like:
NVIDIA-SMI has failed because it couldn't communicate with the NVIDIA driver. Make sure that the latest NVIDIA driver is installed and running.In that case, go back up and follow the install steps.
If you do have a GPU, the line above will output something like:
Wed Jan 19 22:09:08 2022
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 495.46 Driver Version: 460.32.03 CUDA Version: 11.2 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla P100-PCIE... Off | 00000000:00:04.0 Off | 0 |
| N/A 35C P0 27W / 250W | 0MiB / 16280MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+Getting PyTorch to run on the GPU
Once you’ve got a GPU ready to access, the next step is getting PyTorch to use for storing data (tensors) and computing on data (performing operations on tensors).
To do so, you can use the torch.cuda package.
Rather than talk about it, let’s try it out.
You can test if PyTorch has access to a GPU using torch.cuda.is_available().
1
2
3
# Check for GPU
import torch
torch.cuda.is_available()
TrueIf the above outputs True, PyTorch can see and use the GPU, if it outputs False, it can’t see the GPU and in that case, you’ll have to go back through the installation steps.
Now, let’s say you wanted to setup your code so it ran on CPU or the GPU if it was available.
That way, if you or someone decides to run your code, it’ll work regardless of the computing device they’re using.
Let’s create a device variable to store what kind of device is available.
1
2
3
# Set device type
device = "cuda" if torch.cuda.is_available() else "cpu"
device
'cuda'If the above output "cuda" it means we can set all of our PyTorch code to use the available CUDA device (a GPU) and if it output "cpu", our PyTorch code will stick with the CPU.
If you want to do faster computing you can use a GPU but if you want to do much faster computing, you can use multiple GPUs.
You can count the number of GPUs PyTorch has access to using torch.cuda.device_count().
1
2
# Count number of devices
torch.cuda.device_count()
1Knowing the number of GPUs PyTorch has access to is helpful incase you wanted to run a specific process on one GPU and another process on another (PyTorch also has features to let you run a process across all GPUs).
Getting PyTorch to run on Apple Silicon
In order to run PyTorch on Apple’s M1/M2/M3 GPUs you can use the torch.backends.mps module.
Be sure that the versions of the macOS and Pytorch are updated.
You can test if PyTorch has access to a GPU using torch.backends.mps.is_available().
1
2
3
# Check for Apple Silicon GPU
import torch
torch.backends.mps.is_available() # Note this will print false if you're not running on a Mac
True
1
2
3
# Set device type
device = "mps" if torch.backends.mps.is_available() else "cpu"
device
'mps'As before, if the above output "mps" it means we can set all of our PyTorch code to use the available Apple Silicon GPU.
1
2
3
4
5
6
if torch.cuda.is_available():
device = "cuda" # Use NVIDIA GPU (if available)
elif torch.backends.mps.is_available():
device = "mps" # Use Apple Silicon GPU (if available)
else:
device = "cpu" # Default to CPU if no GPU is available
Putting tensors (and models) on the GPU
You can put tensors (and models, we’ll see this later) on a specific device by calling to(device) on them. Where device is the target device you’d like the tensor (or model) to go to.
Why do this?
GPUs offer far faster numerical computing than CPUs do and if a GPU isn’t available, because of our device agnostic code (see above), it’ll run on the CPU.
to(device) (e.g. some_tensor.to(device)) returns a copy of that tensor. This means the same tensor will exist on both CPU and GPU. To overwrite tensors, reassign them: some_tensor = some_tensor.to(device)Let’s try creating a tensor and putting it on the GPU (if it’s available).
1
2
3
4
5
6
7
8
9
# Create tensor (default on CPU)
tensor = torch.tensor([1, 2, 3])
# Tensor not on GPU
print(tensor, tensor.device)
# Move tensor to GPU (if available)
tensor_on_gpu = tensor.to(device)
tensor_on_gpu
tensor([1, 2, 3]) cpu
tensor([1, 2, 3], device='mps:0')If you have a GPU available, the above code will output something like:
1
2
tensor([1, 2, 3]) cpu
tensor([1, 2, 3], device='cuda:0')
Notice the second tensor has device='cuda:0', this means it’s stored on the 0th GPU available (GPUs are 0 indexed, if two GPUs were available, they’d be 'cuda:0' and 'cuda:1' respectively, up to 'cuda:n').
Moving tensors back to the CPU
What if we wanted to move the tensor back to CPU?
For example, you’ll want to do this if you want to interact with your tensors with NumPy (NumPy does not leverage the GPU).
Let’s try using the torch.Tensor.numpy() method on our tensor_on_gpu.
1
2
# If tensor is on GPU, can't transform it to NumPy (this will error)
tensor_on_gpu.numpy()
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell 157 in <cell line: 2>
1 # If tensor is on GPU, can't transform it to NumPy (this will error)
----> 2 tensor_on_gpu.numpy()
TypeError: can't convert cuda:0 device type tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.Instead, to get a tensor back to CPU and usable with NumPy we can use Tensor.cpu().
This copies the tensor to CPU memory so it’s usable with CPUs.
1
2
3
# Instead, copy the tensor back to cpu
tensor_back_on_cpu = tensor_on_gpu.cpu().numpy()
tensor_back_on_cpu
array([1, 2, 3])The above returns a copy of the GPU tensor in CPU memory so the original tensor is still on GPU.
1
tensor_on_gpu
tensor([1, 2, 3], device='cuda:0')Exercises
- Documentation reading - A big part of deep learning (and learning to code in general) is getting familiar with the documentation of a certain framework you’re using. We’ll be using the PyTorch documentation a lot throughout the rest of this course. So I’d recommend spending 10-minutes reading the following (it’s okay if you don’t get some things for now, the focus is not yet full understanding, it’s awareness). See the documentation on
torch.Tensorand fortorch.cuda. - Create a random tensor with shape
(7, 7). - Perform a matrix multiplication on the tensor from 2 with another random tensor with shape
(1, 7)(hint: you may have to transpose the second tensor). - Set the random seed to
0and do exercises 2 & 3 over again. - Speaking of random seeds, we saw how to set it with
torch.manual_seed()but is there a GPU equivalent? (hint: you’ll need to look into the documentation fortorch.cudafor this one). If there is, set the GPU random seed to1234. - Create two random tensors of shape
(2, 3)and send them both to the GPU (you’ll need access to a GPU for this). Settorch.manual_seed(1234)when creating the tensors (this doesn’t have to be the GPU random seed). - Perform a matrix multiplication on the tensors you created in 6 (again, you may have to adjust the shapes of one of the tensors).
- Find the maximum and minimum values of the output of 7.
- Find the maximum and minimum index values of the output of 7.
- Make a random tensor with shape
(1, 1, 1, 10)and then create a new tensor with all the1dimensions removed to be left with a tensor of shape(10). Set the seed to7when you create it and print out the first tensor and it’s shape as well as the second tensor and it’s shape.
Extra-curriculum
- Spend 1-hour going through the PyTorch basics tutorial (I’d recommend the Quickstart and Tensors sections).
- To learn more on how a tensor can represent data, see this video: What’s a tensor?